Расчет передаточной функции системы. Определение устойчивости

Преобразуем функциональной схемы, представленную в соответствии с рисунком 1, в структурную схему на основе передаточных функции полученных в пункте 2. Структурная схема локальной системы автоматического управления громкостью звука с рисунком 8.

Рисунок 8 - Структурная схема САУ громкостью звука

Передаточная функция микрофона имеет вид:

(60)

Передаточная функция промежуточного усилителя имеет вид:

(61)

Передаточная функция микропроцессора имеет вид:

(62)

Передаточная функция делителя напряжения имеет вид:

(63)

Передаточная функция усилителя мощности звуковой частоты имеет вид:

(64)

Передаточная функция акустической системы имеет вид:

(65)

Выделим в структурой схеме изменяемую и неизменяемую части системы автоматического управления.

Изменяемая часть состоит из ЭВМ, в состав которой входят микропроцессор, АЦП и ЦАП. Неизменяемая часть состоит из микрофонов, промежуточных усилителей, делителя напряжения, УМЗЧ и акустической системы.

Передаточная функция замкнутой системы имеет вид:

(66)

Преобразование данной передаточной функции в программе MathCAD:

(67)

Характеристическое уравнение передаточной функции в замкнутом состоянии имеет вид:

(68)

Проверим устойчивость неизменяемой части системы автоматического управления громкостью звука. Так как характеристическое уравнение системы имеет высокий порядок, то проверку устойчивости проведем, используя критерий Михайлова.

Для того, чтобы систему можно было считать устойчивой по Михайлову, необходимо и достаточно, чтобы вектор D (jw), описывающий своим концом кривую Михайлова при изменении частоты от 0 до +¥, начав свое движение с положительной действительной оси и вращаясь против часовой стрелки последовательно проходил n квадрантов, нигде не обращаясь в 0 [13].

В характеристическом уравнении сделаем замену :

(69)

Выделим действительную и мнимую части:

(70)

На плоскости U, jV кривая Михайлова будет иметь следующий вид.

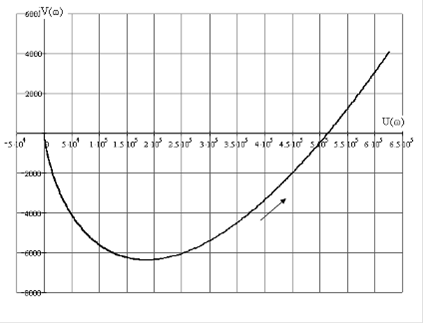
Рисунок 9 - Кривая Михайлова замкнутой САУ

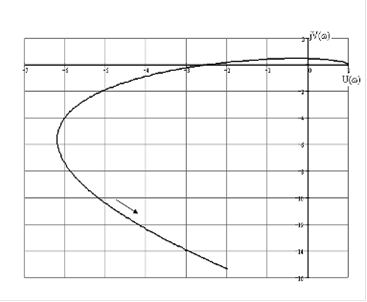
Рисунок 10 - Фрагмент кривой Михайлова для

В данном случае кривая Михайлова начинается в точке (1,0), т.е. на положительной действительной оси, и уходит в бесконечность в 5-м квадранте, двигаясь к которому против часовой стрелки, нигде не обращается в 0. Следовательно, систему можно считать устойчивой по критерию Михайлова.

Построение переходного процесса САУ регулирования громкостью звука выполняется на основе обратное преобразования Лапласа от передаточной функции системы автоматического регулирования в замкнутой форме. Преобразование по Лапласу от передаточной функции системы автоматического регулирования в замкнутой форме осуществляется в программе MathCAD:

Статья в тему

Структурные схемы надежности
Расчёты надёжности - это расчёты, предназначенные для определения количественных показателей надёжности. На этапе проектирования расчёт надёжности проводится с целью прогнозирования надёжности проектируемой системы. На этапе испытаний и эксплуатации расчёт надёжности проводится д ...