Исследование устойчивости по критерию Михайлова

Критерий Михайлова является геометрической интерпретацией принципа аргумента и позволяет судить об устойчивости системы по некоторой кривой, которая называется кривой Михайлова.

Для того, чтобы САУ была устойчива, необходимо, чтобы действительная часть полинома Михайлова D(jw)= была U(0)>0 и çw=0> 0 и достаточно, чтобы корни действительной части U()=0:1, 3, 5 и корни мнимой части =0: 0, 2, 4 были действительные и перемежающиеся, то есть эти частоты чередовались.

Запишем передаточную функцию замкнутой системы:

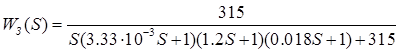(65)

Откуда характеристический полинов будет равен:

(66)

Раскрыв скобки, получим:

(67)

Преобразуем полученное уравнение по Фурье (S→jω) при этом подставив:

(68)

(69)

Вещественная и мнимая части будут соответственно:

(70)

(71)

Проверяем выполнение условий:

(0) > 0; (72)

çw=0> 0; (73)

> 0;

Найдем корни характеристического полинома. Для этого прировняем вещественную и мнимую части к нулю.

(74)

(75)

(76)

(77)

(78)

(79)

(80)

(81)

(82)

(83)

(84)

(85)

Найденые корни:

<129,29<6,244<16,27

Найденные корни не являются перемежающимися (т.е. между любыми двумя соседними корнями U(ω)=0 лежит не корень V(ω)=0 и наоборот). Следовательно, система по критерию Михайлова неустойчива.

Статья в тему

Электромеханический следящий привод робота
Разработать электромеханический следящий привод «плечевой» степени подвижности двухзвенного плоского манипулятора робота, кинематическая схема которого изображена на рис. 1. Рис 1. Расчётная кинематическая схема манипуляционного механизма. Основные технические требова ...