Построение АЧХ и ФЧХ спектра периодического сигнала

Для анализа сигналов и их обработки важное значение имеет разложение заданной функции по различным ортогональным системам. Бесконечная система действительных функций называется ортогональной на отрезке , если При этом предполагается, что , т.е. ни одна из функций рассматриваемой системы не равна тождественно нулю.

Если существует система непрерывных ортогональных функций , то произвольная кусочно-непрерывная функция , для которой выполняется условие абсолютной интегрируемости, т.е. , иметь конечное число максимумов и минимумов, а также конечное число разрывов на каждом конечном интервале, то такая функция может быть представлена в виде суммы обобщенного ряда Фурье

В котором коэффициенты называются спектральными составляющими сигнала и определяются

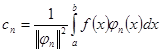
Наибольшее распространение получила ортогональная система основная на тригонометрических функциях - синусах и косинусах. Это объясняется рядом причин. Во-первых, гармоническое колебание является единственной функцией времени, которая сохраняет свою форму при прохождении через любую линейную цепь (с постоянными параметрами). Изменяются лишь амплитуда и фаза колебания. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических сигналов через линейные цепи.

Переходя к функциям времени и учитывая, что функция , аппроксимирующая заданный сигнал, периодическая, то ее можно представить в виде суммы ряда Фурье в тригонометрической форме, коэффициенты которого вычисляются по формулам

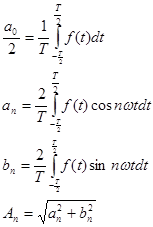где Т - интервал ортогональности совпадающий с периодом функции , а - частота основной гармоники.

Совокупность коэффициентов , характеризующих амплитуды гармонических составляющих, называется амплитудно-частотным спектром периодического сигнала.

Фаза n - ой гармоники, характеризующую фазу спектральных составляющих, определяется по формуле:

Так как сигнал периодический, он имеет линейчатый спектр, представленный набором гармоник с частотами, кратными частоте основной гармоники. Значения вычисленных 25 гармоник, соответствующих АЧХ, ФЧХ и частоты приведены в таблице 5.

Таблица 5

Значения коэффициентов ряда Фурье, АЧХ и ФЧХ сигнала

n	a(n), mV	b(n), mV	A(n), mV	Q(n), рад	w, рад/с
0	14,2000	0,0000	14,2	0	0,00
1	1,7597	9,7025	9,860815	-1,39138	2,69
2	-1,4792	0,3752	1,526002	0,248437	5,37
3	-4,7311	9,4298	10,55003	1,105776	8,06
4	-13,8500	9,7011	16,90959	0,611022	10,74
5	-3,1627	-3,7730	4,923199	-0,87317	13,43
6	-2,9173	-20,1200	20,33039	-1,42681	16,11
7	8,3018	14,5300	16,73443	-1,0517	18,80
8	-6,5793	-1,1721	6,68287	-0,17629	21,48
9	0,6200	-7,6708	7,695838	1,490142	24,17
10	2,5093	3,1108	3,996666	-0,89202	26,85
11	-0,6829	0,6483	0,941618	0,75943	29,54
12	1,3157	-0,7976	1,538538	0,544995	32,22
13	-1,6842	0,8245	1,875151	0,455249	34,91
14	0,5239	0,0008	0,523904	-0,00146	37,59
15	0,3592	-0,4626	0,585672	0,910597	40,28
16	-0,4881	0,4553	0,667455	0,750668	42,96
17	-0,6151	0,6110	0,866995	0,782084	45,65
18	0,1154	-1,1905	1,196076	1,474196	48,33
19	0,1920	-0,2322	0,301319	0,879784	51,02
20	0,0618	0,6214	0,624441	-1,47164	53,70
21	-0,2227	0,1874	0,291055	0,699382	56,39
22	-0,1369	-1,3022	1,309337	-1,46604	59,07
23	0,7937	0,7439	1,087841	-0,75302	61,76
24	-0,4100	0,6026	0,728876	0,973406	64,44
25	-0,1775	-0,7987	0,818189	-1,35212	67,13

Перейти на страницу: 1 2

Статья в тему

Модуляционно-легированные транзисторы MODFET, биполярные транзисторы на гетеропереходах. Резонансный туннельный эффект
Высокая степень интеграции, характерная для современной кремниевой технологии, не может быть достигнута при использовании полупроводниковых соединений AIIIBV, однако эти соединения обеспечивают большее быстродействие, прежде всего, за счет высокой подвижности р носителей и меньши ...

Главные разделы