Ротационный метод вискозиметрии

Ротационный метод вискозиметрии заключается в том, что исследуемая жидкость помещается в малый зазор между двумя телами, необходимый для сдвига исследуемой среды. Одно из тел на протяжении всего опыта остаётся неподвижным, другое, называемое ротором ротационного вискозиметра, совершает вращение с постоянной скоростью.

Очевидно, что вращательное движение ротора визкозиметра передается к другой поверхности (посредством движения вязкой среды; отсутствие проскальзывания среды у поверхностей тела предполагается, таким образом рассматриваются). Отсюда следует тезис: момент вращения ротора ротационного вискозиметра является мерой вязкости. Для простоты мы рассмотрим инверсную модель ротационного вискозиметра: вращаться будет внешнее тело, внутренее тело останется неподвижным, ему и будет сообщаться момент вращения. Однако для краткости изложения будем называть внутреннее тело ротором ротационного вискозиметра. На рисунке 6 расположено схематическое изображение ротационного вискозиметра.

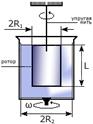
Рисунок 6 - Схематическое изображение ротационного вискозиметра

Введём необходимые обозначения:,L - радиус и длина ротора ротационного вискозиметра;

ω - постоянная угловая скорость вращения внешнего тела;- радиус вращающегося резервуара ротационного вискозиметра;

η - вязкость исследуемой cреды;- момент вращения, передаваемый через вязкую жидкость, равный

,l - диаметр и длина упругой нити,

φ - угол, на который закручивается неподвижно закреплённая нить,- момент упругости материала нити

При этом крутящий момент M1 ротора ротационного вискозиметра уравновешивается моментом сил упругости нити М2:

.

Заметим вновь, что М1=М2, откуда после нескольких преобразований относительно η имеем:

, или

,

где k - постоянная ротационного вискозиметра.

Если рассматривать ту же задачу для ротационного вискозиметра с вращающимся внутренним (ротором висозиметра) и неподвижным внешним телами, имеем:

, или

В этом случае G - момент, необходимый для поддержания постоянной частоты вращения, (один оборот ротора вискозиметра за τ с).

Заметим, что полученные отношения справедливы для цилиндра бесконечной длины, в реальных условиях учитывается поправка на размеры тел ротационного вискозиметра.

Для этого производится вычисление так называемой эффективной высоты H ротационного вискозиметра:

. проводится измерение момента для жидкостей с различным значением вязкости (η1 и η2) при двух различных высотах внутреннего цилиндра (L1 и L2);

. экстраполяцией прямых М1 = f(L) и М2 = f(L) к нулевому значению М1 и М2 получают величину ∆L;

Статья в тему

Строительство волоконно-оптической линии связи на участке Чулым–Колывань
  Опыт строительства ВОЛС в России и странах СНГ выявил ряд существенных отличий в организации, технологии поведения линейных и монтажных работ по сравнению с работами на традиционных электрических кабелях связи. Эти отличия в значительной степени обусловлены тем, что у ОК в отличие от электри ...