Расчет передаточной функции сар. определеие устоичивости

Запишем передаточные функции элементов системы:

Передаточная функция микропроцессора имеет вид:

W(P) = 1.

Передаточная функция двигателя постоянного тока имеет вид:

.

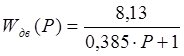Передаточная функция сельсинов имеет вид:

W с (P) = 108

Передаточная функция редуктора имеет вид:

Wр(P) = 0,0036.

Передаточная функция усилительно-преобразовательного устройства имеет вид:

Wуп(P) =

Выделим в структурой схеме изменяемую и неизменяемую части системы автоматического регулирования. Изменяемая часть состоит из ЭВМ, в состав которой входят микропроцессор, АЦП и ЦАП. Неизменяемая часть состоит из усилителено-преобразовательного устройства, двигателя постоянного тока, редуктора и пары сельсин-датчик - сельсин-приёмник.

Функциональная схема неизменяемой части локальной системы регулирования имеет вид в соответствии с рисунком 4:

Рисунок 4 - Функциональная схема локальной системы регулирования неизменяемой части

Передаточная функция замкнутой системы имеет вид:

.

Преобразование данной передаточной функции в программе MathCAD:

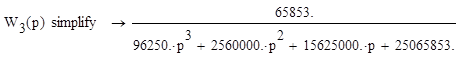
Характеристическое уравнение передаточной функции в замкнутом состоянии имеет вид:

= А0×P3 + А1×P2 + А2×P+А3.

Поверка устойчивости неизменяемой части локальной системы регулирования выполняется на основании критерия устойчивости Гурвица. Для того чтобы система была устойчива необходимо и достаточно, чтобы все определители Гурвица были положительными.

Составление определителей Гурвица и их его вычисление имеют вид:

.

.

.

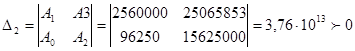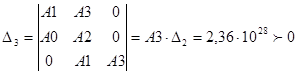Построение переходного процесса выполняется на основе обратное преобразования Лапласа от передаточной функции системы автоматического регулирования в замкнутой форме. Преобразование по Лапласу от передаточной функции системы автоматического регулирования в замкнутой форме осуществляется в программе MathCAD

Графическое представление переходного процесса представлено в соответствии с рисунком 5.

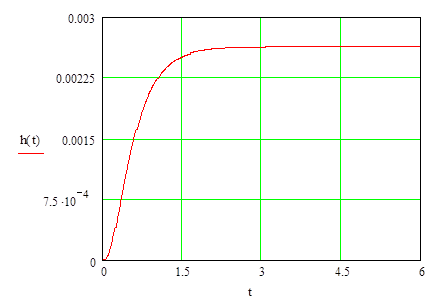
Рисунок 5 - График переходного процесса системы

Показатели качества определяются по графику 9 переходного процесса исходной системы автоматического регулирования

1. s = - перерегулирование.

. n = 0 - число полных колебаний

. tmax = 1,47 - время достижения максимального значения, сек.

. tр = 1,47 - время регулирования, сек.

Проверка устойчивости локальной системы регулирования с учетом ЭВМ выполняется на основании критерия устойчивости Шур - Кона, который позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме z-преобразования.

Замкнутая система будет устойчива, если корни характеристического уравнения будут находиться внутри единичной окружности, т.е., если коэффициенты уравнения будут удовлетворять всем определителям Шур - Кона, имеющих отрицательные значения для нечетных определителей и положительных для четных.

Переход от операторной формы записи передаточной функции замкнутой системы к z- форме и расчет определителей Шур - Кона осуществляется при помощи математического редактора MathCAD.

Разложение передаточной функции замкнутой САР выполняется в программе MathCAD:

.

Переход от операторной формы к z -форме выполняется по формуле (учитывая, что разрядности ЦАП и АЦП равны):

Wз (z) =

- фиксатор нулевого порядка

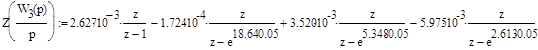
z -форма непрерывной части системы автоматического регулирования.

Передаточная функция в z-форме имеет вид

Полученное выражение преобразуется в программе MathCAD:

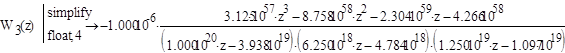
Проверка устойчивости передаточной функции в z - форме выполняется по корням характеристического уравнения.

Характеристическое уравнение в z - форме имеет вид:

Статья в тему

Устройства контроля прозрачности жидкости
На сегодняшний день качество выпускаемой продукции выступает как важнейшая характеристика производства, которая определяет эффективность технологии и оборудования, структуру и организацию управления. Создание качества продукции осуществляется на стадиях всего производственного пр ...