Метод синтеза дискретно-непрерывных систем управления по эталонным моделям движений

,(5.8)

Где

.

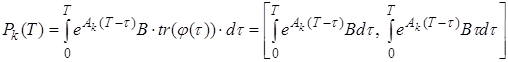где функция транспонирования.

Рассмотрим вычисление компонент матрицы при формировании линейного управляющего воздействия на каждом шаге дискретизации по времени с помощью системы линейно-независимых функций.

Поскольку для линейного управляющего воздействия требуются 2 линейно-независимые функции, то матрица имеет два столбца.

Таким образом, поскольку 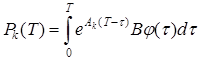, то первый столбец матрицы равен

;

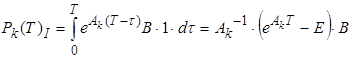второй равен

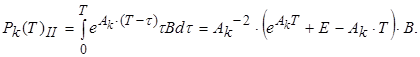
При формировании ступенчатого управляющего воздействия на каждом шаге дискретизации по времени.

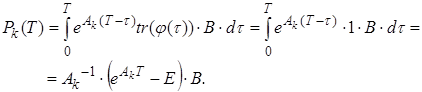
Синтез ЗУ сводится к нахождению последовательности постоянных на каждом шаге квантования по времени вектор-столбцов управления . При этом минимизируется критерий качества, характеризующий отклонения переходного процесса от эталонного в моменты дискретизации

,(5.9)

Где и - соответственно, вектор состояния в синтезированной системе управления и вектор эталонного состояния размерности в момент времени .

Эталонный переходный процесс может быть задан в виде любой непрерывной вектор-функции размерности , например,

,(5.10)

где - матрица размерности , обеспечивающая необходимые показатели качества управления.

При этом ограничение на управляющее воздействие имеет вид:

.(5.11)

Синтез линейных дискретно-непрерывных систем с учетом ограничений [2] в выше приведенной постановке может быть сведен к решению задачи о наименьших квадратах с линейными ограничениями-неравенствами, которая формулируется следующим образом [8,11]: минимизировать

(5.12)

при условии ,(5.13)

где ¾ соответственно - матрица; - вектор неизвестных; - вектор; - матрица; - вектор.

Статья в тему

Трассовый обзорный радиолокатор
Радиолокация - это область науки и техники, объединяющая методы и средства обнаружения, измерения координат, а также определение свойств и характеристик различных объектов, основанных на использовании радиоволн. В процессе радиолокационного наблюдения мы получаем радиолокационную ...