Разработка общей структуры системы управления промышленным роботом

Особенности управления роботом как механической системой

Типовые структуры систем управления промышленными роботами

3.3 Реализация управления роботом на исполнительном уровне

3.4 Датчики обратных связей промышленного робота

4.1.2 Обратная задача о положении манипулятора

4.2 Решение прямой задачи динамики

4.3 Математическая модель электродвигателя постоянного тока

.3 Математическая модель электродвигателя постоянного тока

.1.2 Обратная задача о положении манипулятора

С помощью этой задачи определяют обобщенные координаты qi (i=l,2, ., п) манипулятора по заданному в опорной системе координат положению рабочего органа или некоторого звена манипулятора. В частности, если по заданным координатам схвата rj (j=1, 2, .,т), удается определить обобщенные координаты манипулятора, то координаты других звеньев манипулятора находят на следующем этапе путем решения прямой задачи.

Для данного робота обратную задачу можно решить аналитически. Решение имеет вид:

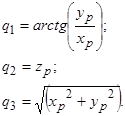(4.1)

Решение прямой задачи динамики

При исследовании динамики манипуляторов составляют расчетную динамическую модель, учитывающую не только геометрические размеры звеньев и распределение кинематических пар, как при составлении кинематической модели, но и распределение масс звеньев и других элементов манипулятора, участвующих в движении. Могут быть учтены и другие свойства манипулятора, например упругие свойства его элементов. В этом случае число степеней свободы системы становится больше числа степеней подвижности манипулятора, которое определяют как число независимых управляемых движений манипулятора (для манипуляторов с разомкнутой кинематической цепью оно равно числу приводов).

В аналитической механике имеются различные принципы и методы для составления дифференциальных уравнений движения механических систем любой сложности. Далее будем использовать уравнения Лагранжа второго рода [19].

,(4.2)

где L - функция Лагранжа (L=K-P); K и P - полные кинетическая и потенциальная энергия системы; qi - обобщенные координаты; - первая производная по времени обобщенных координат; Qi - обобщенные силы (силы или моменты, развиваемые приводами, а также внешние силы или моменты, например возникающие при взаимодействии инструмента и обрабатываемой поверхности), создаваемые в i-м сочленении для реализации заданного движения i-го звена.

Запишем уравнение (5.1) в векторно-матричной форме:

(4.3)

где A(q) - матрица инерционных коэффициентов, зависящих от обобщенных координат; - вектор сил и моментов сил инерции, зависящих от обобщенных координат и скоростей; С(q) - вектор сил и моментов сил тяжести; Q - вектор обобщенных сил.

Рассмотрим степени подвижности манипулятора со структурной схемой, приведенной на рисунке 5.1 по координатам . Звенья манипулятора имеют массы . Размеры рабочего органа считаются существенно малыми по сравнению с остальными линейными размерами манипулятора. Составим уравнения движения манипулятора, считая все элементы абсолютно твердыми телами. Рука считается однородным стержнем длиной и массой . Рабочий орган представляет собой точечную массу .

Кинетическая энергия манипулятора представляет собой сумму кинетических энергий отдельных частей:

, (4.4)

где - кинетическая энергия i-го звена; - кинетическая энергия рабочего органа.

Кинетические энергии для звеньев и рабочего органа равны:

;

;

Статья в тему

Система регулирования печи
автоматизация печь микропроцессорный контроллер Объектом автоматизации является печь для сжигания органических отходов. Как видно из рисунка 1, в топку печи через регулирующие органы подаются отходы, воздух и газ. Причем наносить управляющие воздействия можно при помощи регулирующих о ...