Аппроксимация степенным полиномом

Этот способ аппроксимации основан на разложении нелинейной ВАХ в ряд Тейлора в окрестности рабочей точки „u0”

Если под нелинейным элементом подразумевается транзистор, то i - ток коллектора, а u - напряжение, например, между базой и эмиттером.

В зависимости от амплитуды входного воздействия, формы ВАХ, положения рабочей точки „u0” на ВАХ степенной полином часто удаётся упростить, используя для описания несколько членов ряда.

ВАХ нелинейного элемента задана в табличной форме:

Таблица 6

Координаты ВАХ нелинейного элемента

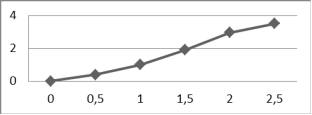
Рисунок 60 - ВАХ нелинейного элемента

Аппроксимируем заданнаю ВАХ полиномом второй степени. Найдем уравнение аппроксимирующей функции по 3-м точкам с координатами (1; 1.0), (1.5; 1.9), (2; 2.95). Рабочая точка нашего сигнала Е0=1,4 В и отклонение в 0.13В мало и диапазон изменения значений напряжения сигнала полностью входит в выбранный для аппроксимации участок ВАХ, следовательно такая аппроксимация для данного вида сигнала будет наиболее точной. Выбор степенной аппроксимации обусловлен малыми значениями сигнала.

Аппроксимируем ВАХ НЭ с помощью полинома второй степени в окрестностях рабочей точки Е0=1,4 В.

Аппроксимацию проведём в пакете Маткад.

Для нахождения коэффициентов а0,а1,а2 нужно решить систему уравнений:

Решим систему уравнений методом Крамера.

Представим систему уравнений в матричном виде

(A)*(B)=(D),

Где матрица А:

матрица В:

,

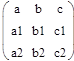Матрица D:

Тогда коэффициенты:

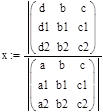
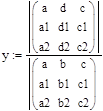
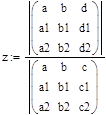
Где а0=x, a1=y, a2=z.0=1.708, a1=1.89, a2=0.3

Получим:

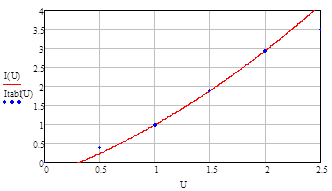
Рисунок 54 -ВАХ, аппроксимированная полиномом второй степени (I(U))

Пусть на вход нелинейного элемента поступает гармоническое колебание с параметрами: A=0.13В, U0=1.4B, f=18кГц, w=2∙π∙f.

Построим его график:

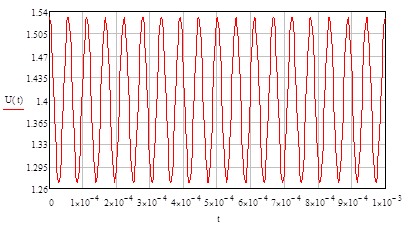
Рисунок 63 - Сигнал на входе НЭ

Применив тригонометрические преобразования, сигнал на выходе НЭ запишем в следующей форме:

U(t) = U0 + A·cos(wt)(t) - U0 = A·cos(wt)= 1.708 a1 = 1.89 a2=0.3= 0,13 B f=18000 Гц w=2π·18000

I(t)=a2·(U(t) - U0)² + a1·(U(t) - U0) + a0 =a2·(A·cos(wt))² + a1·A·cos(wt)

+ a0 = [cos²(wt)=½ + ½·cos(2wt) ] = a2·½·A² + a2·½·A²·cos(2wt) + ·A·cos(wt) +a0 = (a2·½·A² +a0) + a1·A·cos(wt) + a2·½·A²·cos(2wt)

I0 = a2·½·A² +a0 I0 = 1,710535 B= a1·A I1 = 0,2457 B

I2 = a2·½·A² I2 = 0,002535 B

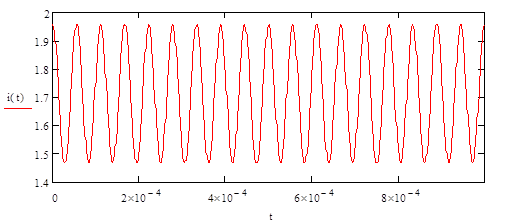
Рисунок 64 - Сигнал на выходе НЭ

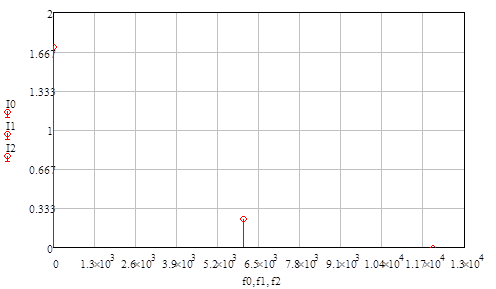
Рисунок 65 - Спектр выходного сигнала

Из рисунка и приведенного выше выражения видны следующие нелинейности ВАХ при гармоническом воздействии:

Статья в тему

Система регулирования печи
автоматизация печь микропроцессорный контроллер Объектом автоматизации является печь для сжигания органических отходов. Как видно из рисунка 1, в топку печи через регулирующие органы подаются отходы, воздух и газ. Причем наносить управляющие воздействия можно при помощи регулирующих о ...