Некоторые свойства преобразований Фурье

Между сигналом s(t) и его спектром S(ω) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из многочисленных возможных преобразований сигнала рассмотрим следующие, наиболее важные: сдвиг сигнала во времени, изменение масштаба времени, сложение сигналов, дифференцирование, интегрирование сигнала.

Сдвиг сигнала во времени

Пусть сигнал s1(t) произвольной формы существует на интервале времени от t1 до t2 и обладает спектральной плотностью S1(ω). При задержке этого сигнала на время t0 получим новою функцию времени s(t2)=s(t - t0), существующую на интервале от t1+t0 до t2+t0.

Спектральная плотность сигнала s2(t) равна

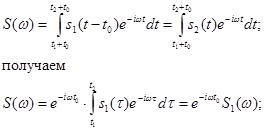
Из этого соотношения видно, что сдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси не зависит.

Сдвиг сигнала во времени осуществляется на величину 0.1Т = 0.234 с

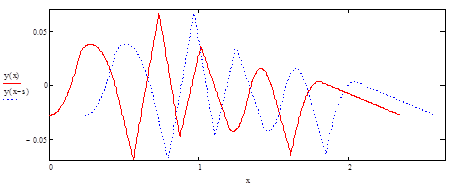
Рисунок 9 - Исходный y(x) и задержанный y(x-to) сигналы

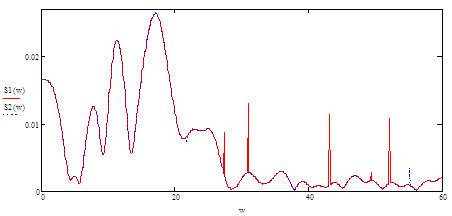
Рисунок 10 -АЧХ исходного S1(ω) и сдвинутого S2(ω) сигналов

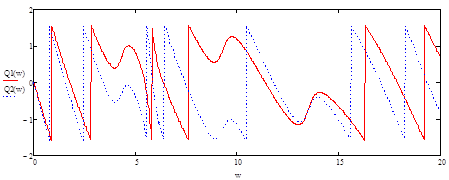
Рисунок 11 - ФЧХ исходного Q1(ω) и сдвинутого Q2(ω) сигналов

Вывод:

Сдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси времени не зависит.

Изменение масштаба времени

Пусть сигнал s1(t) подвергается сжатию во времени. Новый сжатый сигнал s2(t) связан с исходным соотношением s2(t)=s1(nt), n>1.

Спектральная плотность сжатого импульса

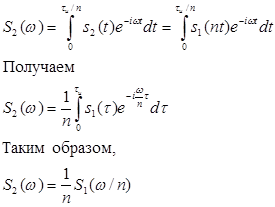
n=2

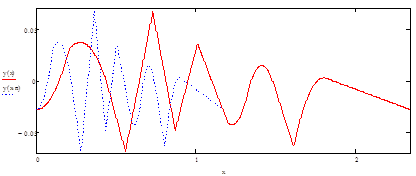
Рисунок 12 - Исходный y(x) и сжатый y(x*n) сигналы

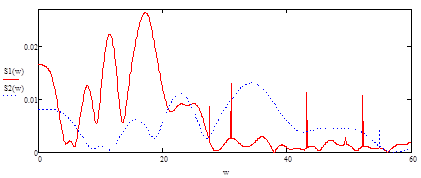
Рисунок 13 - АЧХ исходного S1(w) и сжатого S2(w) сигналов

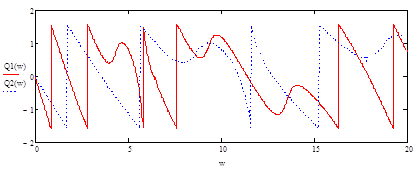
Рисунок 14 - ФЧХ исходного Q1(w) и сжатого Q2(w) сигналов

Вывод:

При сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшится в n раз.

Очевидно, что при растягивании сигнала во времени (т.е. при n<1) имеет место сужение спектра и увеличение модуля спектральной плотности.

Дифференцирование и интегрирование сигнала

Дифференцирование сигнала s1(t) можно трактовать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр. Но производная функции еiωt равна iωeiωt, из чего непосредственно вытекает следующие соответствия:

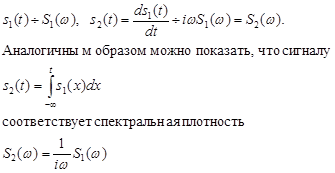
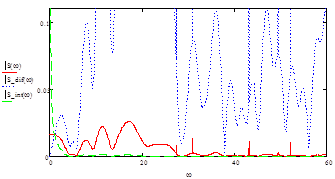
Рисунок 15 - АЧХ исходного S(w), дифференцированного S_dif(w) и интегрированного S_int(w) сигналов

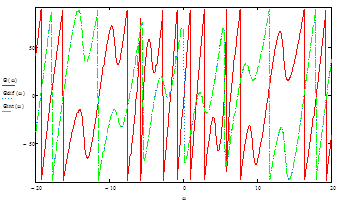
Рисунок 16 - ФЧХ исходного Q(w), дифференцированного Qdif(w), интегрированного Qint(w) сигналов

Сложение с прямоугольным импульсом

Параметры прямоугольного импульса: А=40.5 мВ, τ= 0.36 с, t=0.18с

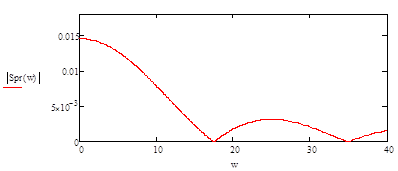
Рисунок 17 - АЧХ прямоугольного импульса

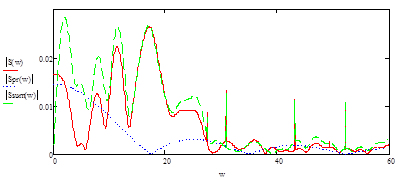
Рисунок 18 - АЧХ исходного сигнала S(w), прямоугольного импульса Spr(w) и суммарного сигнала Ssum(w)

Статья в тему

Система автоматического регулирования захватом руки робота манипулятора
Робот - это универсальный автомат, позволяющий выполнять механические действия. Его принципиальной особенностью является быстрая оперативная перестройка с одной выполняемой операции на другую. Существует несколько разновидностей роботов и для каждого из них имеется своё определение. ...