Измерение радиальной скорости

Радиальной скоростью Vr называют проекцию вектора V скорости цели на направление «измерительная система - цель». Т.к. Vr=dR/dt (где R - расстояние между измерительной системой и целью), в принципе Vr можно определить, дифференцируя показания радиодальномера, либо оценивая конечную разность дальностей на границах фиксированного интервала времени. Однако, повсеместно для измерения скорости Vr используется эффект Доплера а несущей частоте, т.к. при этом обеспечивается несравненно большая точность измерений.

Разность частот излученного и принятого колебаний называется доплеровским приращением частоты fд.

Если передатчик излучает гармонические колебания частоты fд, а приемник движется относительно него с переменной скоростью V(t) под углом Q(t) к линии передатчик - приемник, для большинства практических приложений зависимость f0r от скорости V(t) может быть с удовлетворительной точностью определена простым соотношением:

,

где Vr(t) - радиальная составляющая скорости

l - длина волны излучаемых колебаний

Основная трудность измерения fд в выше беззапросной радиолинии связана с необходимостью иметь в месте приема сигнал, частота которого с высокой точностью (до 10-11-10-10) равна частоте удаленного передатчика. Значительно проще измерять fд в радиолокационной или запросно-ответной системах, в которых передатчик и приемник находятся рядом.

Переход от связного к радиолокационному или запросно-ответному каналам, в которых радиоволны дважды проходят путь между измерительной системой и объектом, дает при прочих равных условиях удвоение приращения доплеровской частоты, т.е.

fд =2Vr(t)/l.

В частном случае прямолинейного равномерного движения, когда V(t)=V0=const, формула для fд упрощается и частота является функцией только угла Q.

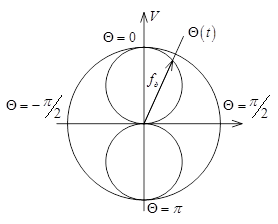
В общем случае эта зависимость характеризуется косинусной полярной диаграммой (рисунок со стр. 12). Из диаграммы видно, что как при сближении, так и при удалении объекта частота fд достигает максимума, когда вектор скорости направлен вдоль радиолуча (Q=0, Q=p) и fд =0 при . При практических расчетах удобно пользоваться формулой

,

где частота выражена в Гц, скорость в м/с, длина волны в см.

Определим порядок доплеровского приращения. Пусть V=103 м/с, l=2 см, Q=0, тогда Гц, при V=102 м/с fд =104 Гц.

Таким образом, в типовых задачах максимальные доплеровские приращения частоты лежат в диапазоне звуковых и ультразвуковых частот.

Статья в тему

Устройство дистанционного измерения параметров аналоговых сигналов
Робототехника и микропроцессорная техника на сегодняшний момент являются одними из самых динамично развивающихся научных и технологических областей человеческого знания. И вследствие развития, усложнения и распространения различных микроконтроллерных устройств появляется необходимость в соответствую ...