Преобразование с помощью разложения сложной структуры по базовому элементу

Этот способ преобразования сложных структурных схем надёжности основан на использовании теоремы о сумме вероятностей несовместных событий, т. е. свойства аддитивности вероятностей.

В соответствии с этой теоремой, если А и В не совместные события, а событие С = А + В, то справедливо равенство

(C) = P(A+B) = P(A)+P(B).

В сложной структурной схеме выбирают базовый элемент или группу базовых элементов, которые не позволяют применить для преобразования структурной схемы основные правила преобразования параллельно-последовательных структур.

Для выбранных элементов делают следующие допущения:

. Базовый элемент находится в работоспособном состоянии на всём интервале времени (через него проходит сигнал), вероятность безотказной работы элемента P(t) =1, при 0≤ t ≤ ∞ .Такой элемент на структурной схеме надёжности может быть заменён «перемычкой».

. Базовый элемент находится в неработоспособном состоянии на всём интервале времени (через него не проходит сигнал), вероятность безотказной работы элемента P(t) = 0, при 0 ≤ t ≤ ∞. Такой элемент на структурной схеме надёжности может быть исключён.

Для этих случаев, представляющих собой два несовместных события, исходная схема надёжности преобразуется в две новые схемы.

Рассмотрим, для примера, сложную структурную схему, представленную на рис. 5.10.

Очевидно, структурная схема надёжности, соответствующая первому допущению (событие А), должна быть дополнена последовательно включённым звеном, имеющим вероятность безотказной работы базового элемента, как показано на рис. 13, а.

а) событие А

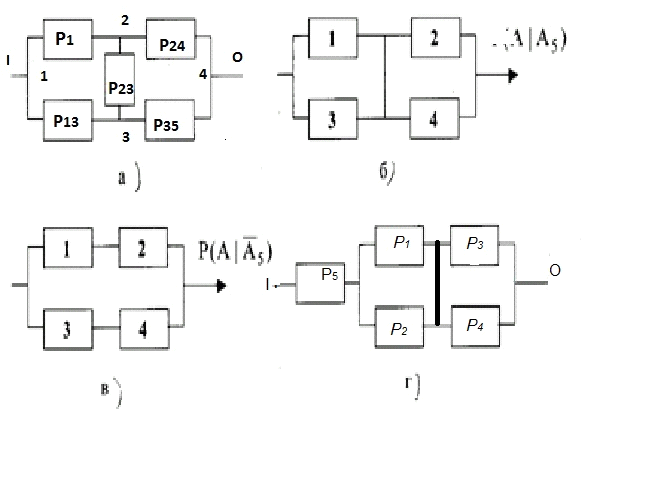
б) событие В

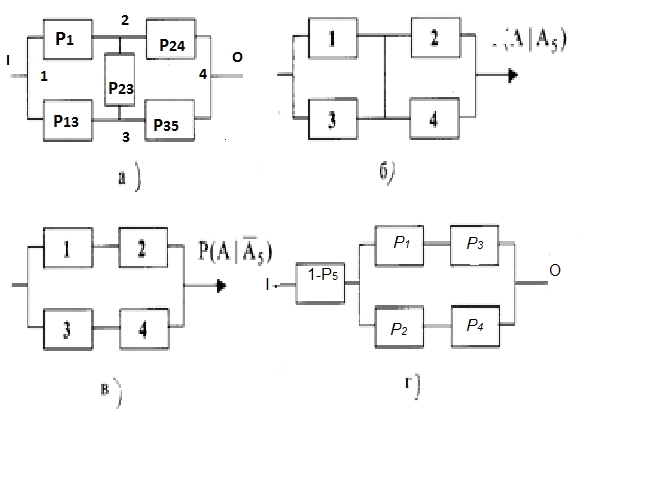
Рисунок - 13. «Предельные» структурные схемы надёжности

Структурная схема надёжности, соответствующая второму допущению (событие В), должна быть дополнена последовательно включённым звеном, имеющим вероятность отказа базового элемента.

Затем находятся формулы для вероятностей безотказной работы каждой из схем, проводится их суммирование и получается итоговая формула для вероятности безотказной работы сложной структурной схемы надёжности.

ЗАКЛЮЧЕНИЕ

В данной работе были рассмотрены основные этапы расчета надежности элементов и систем.

Расчеты показателей безотказности технических систем (ТС) обычно проводятся в предположении, что как вся система, так и любой ее элемент могут находиться только в одном из двух возможных состояний - работоспособном и неработоспособном и отказы элементов независимы друг от друга. Состояние системы (работоспособное или неработоспособное) определяется состоянием элементов и их сочетанием. Поэтому теоретически возможно расчет безотказности любой ТС свести к перебору всех возможных комбинаций состояний элементов, определению вероятности каждого из них и сложению вероятно Расчеты показателей безотказности ТС обычно проводятся в предположении, что как вся система, так и любой ее элемент могут находиться только в одном из двух возможных состояний - работоспособном и неработоспособном и отказы элементов независимы друг от друга. Состояние системы (работоспособное или неработоспособное) определяется состоянием элементов и их сочетанием. Поэтому теоретически возможно расчет безотказности любой ТС свести к перебору всех возможных комбинаций состояний элементов, определению вероятности каждого из них и сложению вероятностей работоспособных состояний системы.

Для этого существуют структурные схемы расчета надежности, которые облегчают расчет безотказности технических устройств в целом.

Статья в тему

Устройства контроля прозрачности жидкости
На сегодняшний день качество выпускаемой продукции выступает как важнейшая характеристика производства, которая определяет эффективность технологии и оборудования, структуру и организацию управления. Создание качества продукции осуществляется на стадиях всего производственного пр ...