Построение и исследование математической модели робота как объекта управления

Решение задач кинематики

Для решения задач кинематики необходимо составить расчетную кинематическую модель манипулятора, в основу которой положены имеющиеся геометрические размеры звеньев, а также типы, количество и распределение кинематических пар.

Положение кинематической цепи в пространстве будем определять с помощью обобщенных координат qi (i=l, 2, ., п), характеризующих относительные перемещения в кинематических парах. Для определения положения рабочего органа в пространстве введем координаты rj (j=1, 2, ., n), где m£6.

Прямая задача о положении

Прямую задачу о положении используют при исследовании кинематики и динамики манипуляторов [16].

При решении этой задачи рассчитывают положение рабочего органа, а также звеньев манипулятора по заданным обобщенным координатам qi (i=l, 2, ., n) в кинематических парах.

Если рассчитывают положение рабочего органа, rj (j=1, 2, .,m), то определяют, соответственно, либо координаты схвата rj (j=1, 2, .,m), либо конечное число наборов координат схвата, либо законы изменения координат схвата во времени ri = rj(t) (j=1,2,…m). В общем случае при m=6 в результате расчета координат схвата, как функций времени можно определить уравнение траектории схвата в параметрической (в зависимости от времени) или явной форме и ориентацию схвата вдоль всей траектории.

С помощью прямой задачи можно определить [19]:

геометрические характеристики рабочего пространства и рабочей зоны манипуляторов со сложной кинематической схемой координаты типа точностные характеристики, например погрешности Drj, (j = 1, 2, т) определения координат схвата обусловленные неточным изготовлением элементов манипулятора, либо ошибками Dqi (i=l, 2, ., п) отработки относительных перемещений qi (i=l, 2, ., п) в кинематических парах; сервисные характеристики.

Кинематическая схема манипулятора приведена на рисунке 4.1

Робот имеет одно вращательное и два поступательных сочленения. Положение рабочего органа манипулятора определяется обобщенными координатами. Тогда решение прямой задачи заключается в нахождении координат точки Р манипулятора в декартовой системе координат OXYZ.

Рисунок 4.1 Кинематическая схема манипулятора

Решение прямой задачи имеет вид:

Задача расчета линейных скоростей и ускорений, а также угловых скоростей и ускорений звеньев тесно связана с прямой задачей о положении манипулятора и также может иметь прямую и обратную постановку.

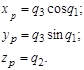
Решение прямой задачи о скоростях для данного манипулятора имеет вид:

Статья в тему

Сигнальные средства связи и современные средства связи в экспедициях
связь сигнализация экспедиция арктический В любой экспедиции, морской или сухопутной, в любом походе или полете может возникнуть чрезвычайная ситуация, в результате которой их участники лишатся всего снаряжения, запасов воды, пищи или значительной их части. Средства радиосвязи - важнейший элемент а ...