Гармоническая линеаризация нелинейности. Расчёт ЗНСАУ частотно-амплитудным методом

Рассмотрим метод гармонической линеаризации. Пусть на вход нелинейного элемента подан гармонический сигнал:

(5.1).

На выходе получим сигнал

(5.2),

который можно разложить в ряд Фурье:

Где - коэффициенты ряда Фурье:

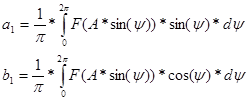
Где .

Примем:

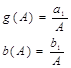
Тогда уравнение (5.2) примет следующий вид:

В области изображений:

Передаточная функция гармонически линеаризованного нелинейного элемента:

Частотная передаточная функция ГЛНЭ:

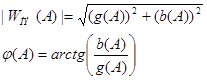
Коэффициенты для нелинейности:

(т.к. нелинейность однозначная).

Определим наличие периодического режима частотно-амплитудным методом.

1. Гармоническая линеаризация нелинейного элемента:

2. Условие существования периодического режима:

(5.3)

Где - АФХ разомкнутой гармонически линеаризованной системы (РГЛС), т.е. используется критерий Найквиста: в замкнутой ГЛНС будет периодический режим, если АФХ РГЛС проходит через точку с координатами .

Уравнение (5.3) в иной форме:

С помощью программы MathCad строим АФХ линейной части и инверсную АФХ нелинейного элемента.

Значение амплитуды от 0 до 300.

Получаем графики Wлч(jщ) и -1/Z НЭ(A):

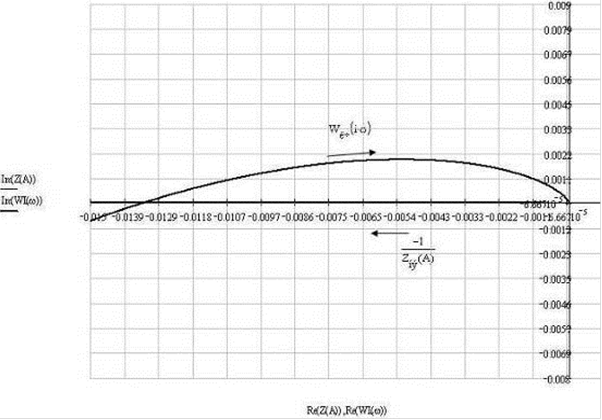
Рис. 6. Определение ПР

Из графика видно (рис. 6), что кривые пересекаются, следовательно, в данном случае периодический режим существует.

Построим кривую , пренебрегая произведением .

Из графика видно (рис. 7), что кривые не пересекаются, следовательно, и в данном случае периодический режим не наблюдается. Значит чем больше значение , то тем круче будет проходить .

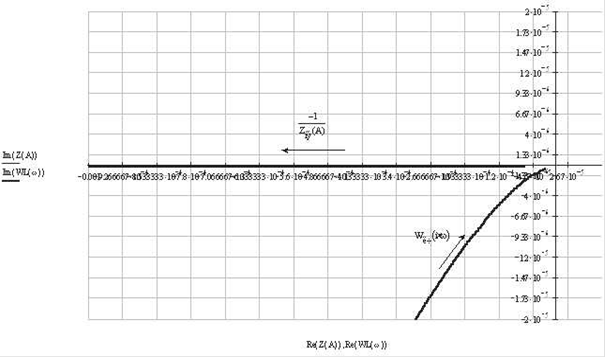
Рис. 7. Определение ПР без

Статья в тему

Параметрический синтез антенны базовой станции по заданным требованиям к диаграмме направленности
Антенной называется радиотехническое устройство, предназначенное для изучения или приема электромагнитных волн. Антенна является одним из важнейших элементов любой радиотехнической системы, связанной с излучением или приемом радиоволн. К таким системам относят: системы радиосвязи, ра ...