Бигармоническое воздействие

На НЭ воздействуют два гармонических сигнала:

Параметры сигналов:

A1=0.13В, f1=18кГц, U01=1,4В

А2=0.09В, f2=22кГц, U02=0В

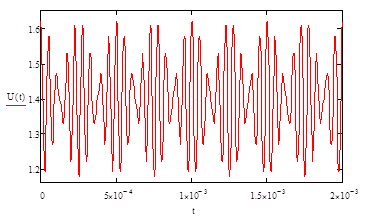
Рисунок 70 - Бигармонический сигнал на входе НЭ

Этот бигармонический сигнал поступает на нелинейный элемент, у которого ВАХ описывается выражением:

Подставив в формулу выражение для бигармонического сигнала, получим сигнал на выходе нелинейного элемента:

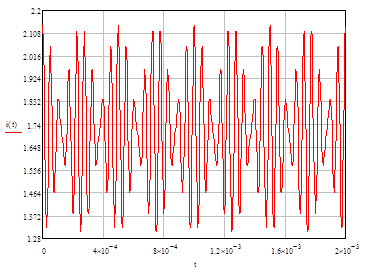
Рисунок 71 - Бигармонический сигнал на выходе НЭ

Для упрощения рассмотрим слабо-нелинейный режим, то есть когда достаточно учитывать только линейный и квадратичный члены полинома.

U(t) = U0 + A1·cos(w1t) + A2·cos(w2t)(t) - U0 = A1·cos(w1t) + A2·cos(w2t)(t) = a2·( U(t) - U0)² + a1·( U(t) - U0) + a0 =

= a2·( A1·cos(w1t) + A2·cos(w2t))² + a1·( A1·cos(w1t) + A2·cos(w2t)) + a0=

= a2·( A1²·cos(w1t) ² + A2²·cos(w2t)2 + 2· A1· A2·cos(w1t)·cos(w2t)) +

+ a1·( A1·cos(w1t) + A2·cos(w2t)) + a0=

[ cos²(wt)=½ + ½·cos(2wt);

cos(w1t) ·cos(w2t) =½·cos(w2t - w1t) + ½·cos(w1t + w2t) ]

= (½·a2·(A1² + A2²) + a0) + a1·A1·cos(w1t) + a1·A2·cos(w2t) + + ½· a2·

A1²·cos(2 w1t) + ½· a2· A2²·cos(2 w2t) + a2· A1· A2·cos(w2t - w1t) +

+ a2· A1· A2·cos(w2t + w1t)

На выходе появляются дополнительные составляющие на комбинационных частотах, которые можно посчитать по формулам:

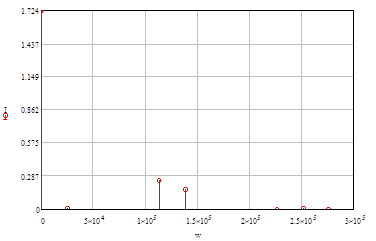
Рисунок 72 - Спектр бигармонического сигнала на выходе НЭ

Статья в тему

Схемы управления и обработки выходного сигнала прибора с зарядовой связью
Фото матрица ПЗС представляет собой микросхему средней интеграции, состоящую из четырёх основных секций - накопления, памяти, нижнего однострочного регистра и выходного устройства. Во время активной части полукадра в секции накопления создается потенциальный рельеф, соответствующий распределению яр ...